Augusto Rufasto

Strategic Intelligence

www.geocities.com/arufast

rufasto2000@gmail.com

Shapley Value

Introduction

Shapley value is a Game Theory concept proposed by Lloyd Shapley in 1953 aiming to propose the fairest allocation of collectively gained profits between the several collaborative agents. The basic criterion is to find the relative importance of every agent regarding the cooperative activities.

Function definition

The characteristic function

Let N be a set of n agents. Let us define the characteristic function v(S) as follows:

The whole set of characteristic functions V(N) is:

The v function has the following properties:

(1)

(2)

Here S and T are disjoint subsets from N. Function v should be interpreted as follows: If S is a coalition of s agents all of which agree to cooperate, then v(S) is the total expected revenue from this S cooperation, regardless of the actions of any agent external to S may do. As stated in the condition of super-additivity, collaboration from agents new to the coalition should increase the revenue to the coalition, but never decrease it.

The allocation function

Let us define the allocation function Φ as:

Given v(N), Φ Hill specify the weight Φ_i for each agent i. The set containing all the Φ_i is the allocation rule for the coalition.

A new agent joins a group of agents

Let’s now consider that there exists one original coalition S and that a new agent called i studies the possibility of joining it. That will imply that i can create value added after joining the group. His contribution should be assessed by the method of comparing the value of the coalition S including i minus the value of the sole coalition S. Afterwards, it will be necessary to build the fair distribution criterion. To do that, we will use the propositions of Shapley.

The marginal contribution of agent i to S

So let’s now compare the value of the new coalition minus the value of the original one. We will assess i’s contribution by calculating:

Total possible coalitions

The total sub-coalitions of s agents (s does not include newcomer agent i) that can be built between the n members of the N set is:

We are interested in formalizing the event of i associating himself with the s members of a group. Consider then that the total possible coalitions with size s that necessarily do not include i is exactly the number of the total possible coalitions size s+1 that do necessarily include i.

When the new agent i is willing to participate in an (n+1)-size coalition, then we may say that s equals n, and therefore the total number of possible coalitions with n+1 members including agent i will be:

Weight factor q(s)

Let us build weight factor q as:

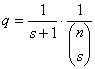
Now, the contribution of new agent i to one specific coalition will be divided by the total number of possible coalitions, that is, his contribution will be multiplied by the following factor:

The coalition of agent i with subset S will therefore get this distributed revenue. But inside a specific subset S there are s agents. The final coalition has therefore (s+1) agents. We need now to distribute the contribution share already allocated to the coalition between (s+1) agents. And in this way we get weight factor q. We may think of q as the area share of a small rectangle which width equals the total number of coalitions that do necessarily include agent I, and which height equals the (s+1) number of agents in such coalition.

Shapley allocation rule Φ_i

Let us consider:

The sum includes all subsets size s that necessarily do not include agent i, that is, the total subsets size (s+1) that do necessarily include agent i.

Shares on the coalition revenues: r_i

Consider agent i analyzes his future collaboration with group S. Let’s call the shares corresponding to i and to each member of group S as r(α_i) y r(α_s). May j be the general notation for agent i and for each member of S. Then, each share rj will be calculated as follows:

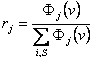
The firm

Consider the possibility of a new firm to be built upon the coalition of one entrepreneur α₀ and m workers α_i. Entrepreneur α₀ cannot generate any value by remaining alone, his role is to supply production means to the workers. All m workers α_i are capable to create a value of B when using the production means offered by α₀. A coalition S which size was k+1 (including the entrepreneur and k workers) will produce a value of kB. Consider now coalition S-α_i which size was k and including only workers, and not the entrepreneur. Its value will be 0. Suppose that all k workers, after joining a group, are looking for an entrepreneur. The entrepreneur’s marginal contribution will then be kB.

Now suppose that all m workers joined that group. Then the size of the coalition will be m+1, and Shapley allocation factor according to the rule are:

for entrepreneur α₀

for any worker α_i

Shares on the coalition revenues: r_i

Let us build the shares that each agent will receive of the coalition revenues, let these shares be called r(α₀) y r(α_i). Each share will be calculated as follows:

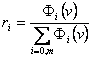
So that calculated shares are:

This means that the entrepreneur gets 50% of the coalition revenue and that the remaining 50% is to be distributed between the m workers.

Calculation of revenues

The revenue for the coalition is mB. Entrepreneur earns:

Each worker earns:

This corresponds to half his marginal contribution to the coalition.

The salary rule

This states a rule for defining salary in a firm. As before, we suppose that the presence of the entrepreneur is necessary for the firm to operate. Let’s say the firm is has now the manager and m employees producing B each one and is also willing to hire a new employee. If, by staying out of the firm the future employee produces zero but entering in the firm he produces C, then the values for the allocation rule are:

So that calculated share factor are:

for entrepreneur α₀

for any worker α_i

for the new employee

The revenue for the coalition is mB+C. Entrepreneur earns:

Each old worker earns:

The new employee earns:

Any agent which joins any coalition under the same conditions described here will deserve to retrieve an income equal to half his marginal contribution:

According to that, if a new employee joins a firm which without his participation cannot generate new incomes, then the new employee’s fair salary will be half his marginal contribution to the firm. Let’s put it this way: if the new employee is capable to generate 200,000 dollars a year within the firm and zero when out of it, then his annual fair salary within the company will be 100,000 dollars. Also note that if this new employee is capable to make money out of the firm, then his fair salary will automatically rise, because the firm’s marginal contribution to his earnings will be smaller.

One reason that may push actual salaries below their fair levels

Having already stated the salary rule, one may think about the differences that can be found in the real world, regarding salaries. The one main reason for these differences is the bargaining power. If a firm has great bargaining power, then new employees will be pushed to accept salaries at any point below the fair level. On the side of the firm, there will appear extraordinary earnings. On the side of the new employee, there will be a relative loss when accepting the salary offered by the firm. The negotiation is performed in a conventional zero-sum-game scenario, so extra earnings in one side are covered by losses on the opposite side.

Appendix: Shapley’s desired properties for a coalition

The following are the desired properties for a coalition (it has been stated that Shapley value is the unique criteria set that has properties 2, 3 and 5):

P1: Advantageous participation in the coalition

For each i in N:

It means that each agent gets from the coalition at least the value he can generate by himself alone.

P2: Efficient allocation

Total revenues are fully allocated between the agents:

P3: Anonymity

Let w be value earned by a coalition which includes an agent called j, and let w be equivalent to v, the value earned by a coalition which includes agent i. Then:

The names of the agents do not affect the allocation of revenues.

P4: Symmetry

For any pair of agents i and j, if, for every S that belongs to 2ⁿ, neither i nor j belong to S, if:

then:

P5: Additivity

If we add the two coalition sets described by earning functions v and w, the earnings’ distribution will be:

This will be valid for every agent i in N.

References

Wikipedia: http://en.wikipedia.org/wiki/Shapley_value, which refers to: Lloyd S. Shapley’s ‘A Value for n-person Games’ in ‘Contributions to the Theory of Games, volume II’, H.W. Kuhn and A.W. Tucker, editors, Annals of Mathematical Studies v. 28, pp. 307-317, Princeton University Press

Augusto Rufasto – Strategic Intelligence

www.geocities/arufast

rufasto2000@gmail.com